EVIDENCIAS PROBABILIDAD Y ESTADISTICA: APUNTAMIENTO

APUNTAMIENTO

El coeficiente de apuntamiento de uso más extendido es el basado en el cuarto momento con respecto a la media y se define como:

$\beta_2=\frac{\mu_4}{\sigma^4}$

donde $\mu_4$ es el 4º momento centrado o con respecto a la media y $\sigma$ es la desviación estándar.

En ocasiones se emplea esta otra definición del coeficiente de curtosis:

$g_2=\frac{\mu_4}{\sigma^4}-3$

donde al final se ha sustraido 3 (que es la curtosis de la Normal) con objeto de generar un coeficiente que valga 0 para la Normal y tome a ésta como referencia de apuntamiento:

Tomando, pues, la distribución normal como referencia, una distribución puede ser:

más apuntada y con colas más anchas que la normal –leptocúrtica.
menos apuntada y con colas menos anchas que la normal- platicúrtica.
la distribución normal es mesocúrtica.

En la distribución normal se verifica que $\mu_4=3\sigma^4$ , donde $\mu_4$ es el momento de orden 4 respecto a la media y $\sigma$ la desviación típica.

Así tendremos que:

Si la distribución es leptocúrtica $\beta_2>3$ y $g_2>0$
Si la distribución es platicúrtica 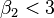$\beta_2<3$ y $g_2<0$
Si la distribución es mesocúrtica 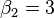$\beta_2=3$ y $g_2=0$

Otra forma de medir la curtosis se obtiene examinando la fórmula de la curtosis de la suma de variables aleatorias. Si Y es la suma de n variables aleatorias estadísticamente independientes, todas con igual distribución X, entonces $Kurt[Y] = \frac{Kurt[X]}{n}$ , complicándose la fórmula si la curtosis se hubiese definido como $\frac{\mu_4}{\sigma^4}$ .

EVIDENCIAS PROBABILIDAD Y ESTADISTICA

domingo, 4 de noviembre de 2012

APUNTAMIENTO

No hay comentarios:

Publicar un comentario

Datos personales